今日头条2018校招算法方向 第一批 链接:here
三道编程题,难度循序渐进,第三题做了很久还是有问题
- 一道求外围点的题
P为给定的二维平面整数点集。定义 P 中某点x,如果x满足 P 中任意点都不在 x 的右上方区域内(横纵坐标都大于x),则称其为“最大的”。求出所有“最大的”点的集合。(所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内)
如下图:实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。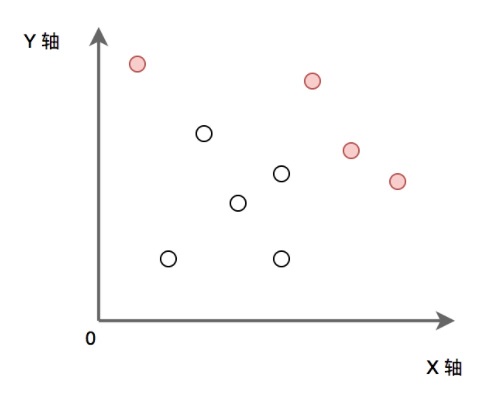
输入描述:
第一行输入点集的个数 N, 接下来 N 行,每行两个数字代表点的 X 轴和 Y 轴。
对于 50%的数据, 1 <= N <= 10000;
对于 100%的数据, 1 <= N <= 500000;输出描述:
输出“最大的” 点集合, 按照 X 轴从小到大的方式输出,每行两个数字分别代表点的 X 轴和 Y轴。输入例子1:
5
1 2
5 3
4 6
7 5
9 0输出例子1:
4 6
7 5
9 0思路如果是暴力枚举的话肯定就超时了,这里要用到一个小技巧,就是对横坐标或是纵坐标排序,然后才进行迭代
还有一个坑就是,输入输出的方式,这里一开始用 cin 和 cout 发现一直是80%AC 改成scanf 和 printf后就是100% :(1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40// 今日头条实习生 第一题 100% AC cin 与 cout 太浪费时间(80%AC) 改用 scanf 和 printf
using namespace std;
bool compare(pair<int,int> a, pair<int,int> b)
{
return a.second > b.second; //升序排列,如果改为return a>b,则为降序
}
int main()
{
int count;
cin>>count;
vector<pair<int,int> > points(count);
for(int i = 0; i < count; ++i)
{
scanf("%d %d", &points[i].first, &points[i].second);
}
sort(points.begin(),points.end(),compare);
pair<int,int> pointTmp = points[0];
vector<int> goodPoints;
for(int i = 0; i < points.size(); ++i)
{
if(points[i].first >= pointTmp.first)
{
goodPoints.push_back(i);
pointTmp = points[i];
}
}
for(auto c : goodPoints)
{
printf("%d %d\n", points[c].first,points[c].second);
}
return 0 ;
} - 一道很像动态规划的单调栈题
给定一个数组序列, 需要求选出一个区间, 使得该区间是所有区间中经过如下计算的值最大的一个:区间中的最小数 * 区间所有数的和最后程序输出经过计算后的最大值即可,不需要输出具体的区间。如给定序列 [6 2 1]则根据上述公式, 可得到所有可以选定各个区间的计算值:
输入描述:
第一行输入数组序列长度n,第二行输入数组序列。
对于 50%的数据, 1 <= n <= 10000;
对于 100%的数据, 1 <= n <= 500000;输出描述:
输出数组经过计算后的最大值。输入例子1:
3
6 2 1输出例子1:
36思路,有一种动态规划的思路,但是AC好像只有40% 原因是内存超出限制
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// 动态规划解法 40% AC 内存超出限制
using namespace std;
int main(int argc, char *argv[])
{
int count;
int tmp;
vector<int> arr;
cin>>count;
while(count-- > 0)
{
cin>>tmp;
arr.push_back(tmp);
}
int num = arr.size();
int maxSum = INT_MIN;
vector<int> sum(num+1);
vector<vector<int> > mindp(num,vector<int>(num));
sum[0] = 0;
for(int i = 1; i < num + 1; ++i)
{
sum[i] = sum[i-1] + arr[i-1];
}
for(int i = 0; i < num; ++i)
{
for(int j = i; j < num; ++j)
{
if(i == j)
mindp[i][j] = arr[i];
else
{
mindp[i][j] = min(mindp[i][j-1],arr[j]);
}
maxSum = max(maxSum,mindp[i][j] * (sum[j+1] - sum[i]));
}
}
cout<<maxSum<<endl;
return 0;
}第二种就是单调栈的解法,大致的思路就是维护一个单调栈,然后每次更新栈的同时更新最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71// 单调栈解法 100% AC
using namespace std;
int vecSum(vector<int> &vec, int begin, int end)
{
if(begin > end)
begin = 0;
int re = 0;
for(int i = begin; i <= end; ++i)
{
re += vec[i];
}
return re;
}
int main(int argc, char *argv[])
{
int count;
int tmp;
vector<int> arr;
cin>>count;
while(count-- > 0)
{
cin>>tmp;
arr.push_back(tmp);
}
int num = arr.size();
int maxSum = INT_MIN;
stack<int> upStack;
arr.push_back(-1); // 先添加一个小于0 的数作为比较,以去除每次非空的判断
upStack.push(num); // 将 最后的那个自行添加的数的下标添加到栈中
int top = 0;
for(int i = 0; i < num; ++i)
{
if(arr[i] >= arr[upStack.top()])// 如果比当前的栈顶的元素要大的话就直接压栈
{
upStack.push(i);
}
// 否则的话就先弹出栈顶的元素,直到满足上面的压栈条件,
// 并且 计算 栈顶元素的单调区间(以栈顶元素开始往前单调递减 但 不小于当前值的 整个区间)的值
// 然后更新 maxSum 的值 并压栈
else
{
while(arr[i] < arr[upStack.top()])
{
top = upStack.top();
upStack.pop();
maxSum = max(maxSum,arr[top] * vecSum(arr,upStack.top()+1,i-1));//弹出栈并更新最大值
}
upStack.push(i);
}
}
int topEnd = upStack.top();
while(upStack.top() != num)
{
top = upStack.top();
upStack.pop();
maxSum = max(maxSum,arr[top] * vecSum(arr,upStack.top()+1,topEnd));//弹出栈并更新最大值
}
cout<<maxSum<<endl;
return 0;
} - 一道任务调度的题 该题较难,没有AC 但是我感觉思路是死的,也没想到啥高端的算法
产品经理(PM)有很多好的idea,而这些idea需要程序员实现。现在有N个PM,在某个时间会想出一个 idea,每个 idea 有提出时间、所需时间和优先等级。对于一个PM来说,最想实现的idea首先考虑优先等级高的,相同的情况下优先所需时间最小的,还相同的情况下选择最早想出的,没有 PM 会在同一时刻提出两个 idea。
同时有M个程序员,每个程序员空闲的时候就会查看每个PM尚未执行并且最想完成的一个idea,然后从中挑选出所需时间最小的一个idea独立实现,如果所需时间相同则选择PM序号最小的。直到完成了idea才会重复上述操作。如果有多个同时处于空闲状态的程序员,那么他们会依次进行查看idea的操作。
求每个idea实现的时间。
输入第一行三个数N、M、P,分别表示有N个PM,M个程序员,P个idea。随后有P行,每行有4个数字,分别是PM序号、提出时间、优先等级和所需时间。输出P行,分别表示每个idea实现的时间点。输入描述:
输入第一行三个数N、M、P,分别表示有N个PM,M个程序员,P个idea。随后有P行,每行有4个数字,分别是PM序号、提出时间、优先等级和所需时间。全部数据范围 [1, 3000]。输出描述:
输出P行,分别表示每个idea实现的时间点。输入例子1:
2 2 5
1 1 1 2
1 2 1 1
1 3 2 2
2 1 1 2
2 3 5 5输出例子1:
3
4
5
3
9能有的思路就是一个死的思路,但是没有AC 贴上代码,这里有个10%AC的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
using namespace std;
class Task {
public:
int idealId;
int pmId;
int timeStart;
int pority;
int timeCost;
int timeFinish;
};
bool compare(Task t1,Task t2)
{
if(t1.pority == t2.pority)
{
if(t1.timeCost == t2.timeCost)
{
return t1.timeStart < t2.timeStart;
}
else
{
return t1.timeCost < t2.timeCost;
}
}
else
{
return t1.pority < t2.pority;
}
}
bool getTask(Task t1,Task t2)
{
if(t1.timeCost == t2.timeCost)
return t1.pmId < t2.pmId;
else
return t1.pmId < t2.pmId;
}
void getPmTask( vector<vector<Task > > & pmdata, vector<Task> & taskPerPm, vector<int> &selectIndex, int & coder)
{
taskPerPm.clear();
Task tmpTask;
int select = 0;
for(int i = 0; i < pmdata.size(); ++i)
{
if(pmdata[i].size() == 0)//该pm已经没有任务可以调度了
{
continue;
}
else
{
if(coder < pmdata[i][0].timeStart)//如果优先级高的需要等待,则优先选择不需要等待的次高优先级的任务 情况一
{
tmpTask = pmdata[i][0];
select = 0;
for(int j = 1; j < pmdata[i].size(); ++j)
{
if(pmdata[i][j].timeStart < tmpTask.timeStart)//待定任务
{
tmpTask = pmdata[i][j];//更新需要等待时间最少的任务
select = j;
if(coder >= pmdata[i][j].timeStart)//找到优先级最高的那个不需要等待的任务
{
taskPerPm.push_back(tmpTask);
selectIndex[i] = select;//更新当先加入队列中的任务
break;
}
}
}
taskPerPm.push_back(tmpTask);//该pm找不到不需要等待的任务
selectIndex[i] = select;
}
else//高优先级,不需要等待,直接进入队列 情况二
{
taskPerPm.push_back(pmdata[i][0]);
selectIndex[i] = 0;
}
}
}
}
void tasklt(int & coder, vector<int> & selectIndex, vector<Task> & taskPerPm, vector<vector<Task > > & pmdata, vector<Task> & data)
{
// 选出需要完成的最高优先级任务
Task tmpTask = taskPerPm[0];
// 并判断coder空闲的时间任务有没有产生,如果没有产生就去获取最先产生的次优先级的任务
if(coder < tmpTask.timeStart)
{
for(int i = 1; i < taskPerPm.size(); ++i)
{
if(tmpTask.timeStart > taskPerPm[i].timeStart)// 选取最先产生的任务
{
tmpTask = taskPerPm[i];
if(coder >= tmpTask.timeStart)//在满足已经产生的情况下,优先级最高的任务 找到了
break;
}
}
}
//完成一个任务 然后更新它的 timeFinish
data[tmpTask.idealId].timeFinish = tmpTask.timeCost + (tmpTask.timeStart > coder ? tmpTask.timeStart : coder);
// 更新coder的工作时长
coder += tmpTask.timeStart > coder ? tmpTask.timeStart : 0;//加上等待时间
coder += tmpTask.timeCost;
// 从pm的待解决任务中移除已经调度的任务
vector<Task>::iterator it = pmdata[tmpTask.pmId].begin()+selectIndex[tmpTask.pmId];
pmdata[tmpTask.pmId].erase(it);
}
int main(int argc, char *argv[])
{
int pmNum, coderNum, idealNum;
cin>>pmNum>>coderNum>>idealNum;
vector<vector<Task > > pmdata(pmNum);
vector<Task > data;
Task tmpTask;
tmpTask.timeFinish = 0;
int idealNumtmp = idealNum;
while(idealNumtmp-- > 0)
{
cin>>tmpTask.pmId>>tmpTask.timeStart>>tmpTask.pority>>tmpTask.timeCost;
tmpTask.idealId = idealNum - idealNumtmp-1;
tmpTask.pmId -= 1;
data.push_back(tmpTask);
pmdata[tmpTask.pmId].push_back(tmpTask);
}
// 先不考虑产生时间, 按照固定的优先级进行排序
for(int i = 0; i < pmNum; ++i)
{
sort(pmdata[i].begin(),pmdata[i].end(),compare);
}
vector<int > coder(coderNum); // 程序员的当前时间点
for(auto c : coder)
{
c = 0;
}
vector<int> selectIndex(pmNum);//当前进入选择队列的下标
vector<Task> taskPerPm;//里面是每个pm最想完成的任务
idealNumtmp = idealNum;
while(idealNumtmp-- > 0) // 对每个任务进行调度
{
// 先从pm处获取任务,分为两种情况,coder空闲时 任务已经产生还是没有产生
getPmTask(pmdata,taskPerPm,selectIndex,coder[0]);
sort(taskPerPm.begin(),taskPerPm.end(),getTask);// 获取优先级最高的任务
tasklt(coder[0],selectIndex,taskPerPm,pmdata,data);// 寻找优先级最高的任务给 最先完成的程序员进行调度
sort(coder.begin(),coder.end());//重新进行排序 以获取先完成的任务coder
}
for(auto c : data)
{
cout<<c.timeFinish<<endl;
}
return 0;
}
